# 动态规划(DP)算法
关键词: 状态转移方程 最优子结构 边界
下面是「动态规划』问题的思考路径:
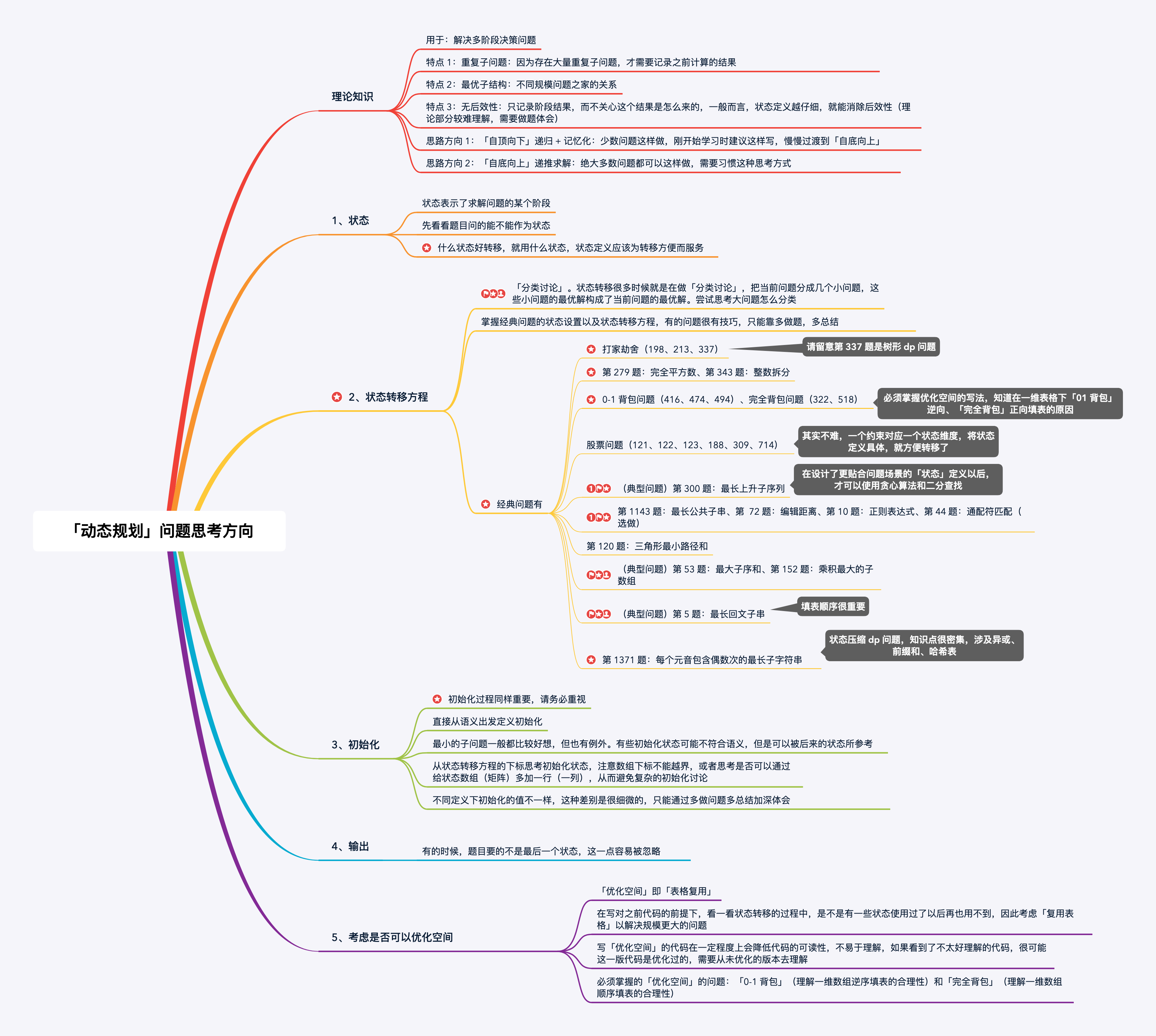
提示
右键「在新便签页打开图片」可查看大图。
# 最长回文子串
给定一个字符串s,找到s中最长的回文子串。你可以假设 s 的最大长度为1000。
# 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬1或 2个台阶。你有多少种不同的方法可以爬到楼顶呢?
动态规划的思路和算法:
用 f(n) 表示爬到第n级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
F(n) = F(n - 1) + F(n - 2),其中 n > 1
1
可知本题是斐波那契数列。
# 斐波那契数列
斐波那契数,通常用F(n)表示,形成的序列称为 斐波那契数列(Fibonacci sequence)。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
1
2
2
给你 n ,请计算 F(n) 。
动态规划解法如下:
class Solution {
public int fib(int n) {
if (n < 2) {
return n;
}
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
复杂度分析
- 时间复杂度:
O(n)。 - 空间复杂度:
O(1)。
# 零钱兑换
# 零钱兑换一:给定不同面额的硬币coins和一个总金额amount。计算可以凑成总金额所需的最少的硬币个数。
状态转移方程:
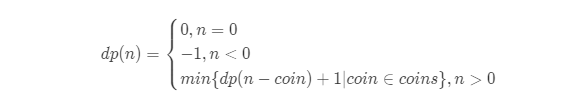
# 零钱兑换二:给定不同面额的硬币和一个总金额。计算可以凑成总金额的硬币组合数。
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int x = coin; x < amount + 1; ++x) {
dp[x] += dp[x - coin];
}
}
return dp[amount];
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
复杂度分析
- 时间复杂度:
O(N×amount)。其中N为coins数组的长度。 - 空间复杂度:
O(amount),dp数组使用的空间。
参考文档
